Inverted Pendulum Parameter Estimation
This example shows how to use Simulink® Design Optimization™ to estimate multiple parameters of a model by iterated estimations.
This example requires Simscape™ Multibody™ software.
Simscape Multibody Model of the Inverted Pendulum System
The Simulink® model for the inverted pendulum, spe_mech_invpend, is shown below.
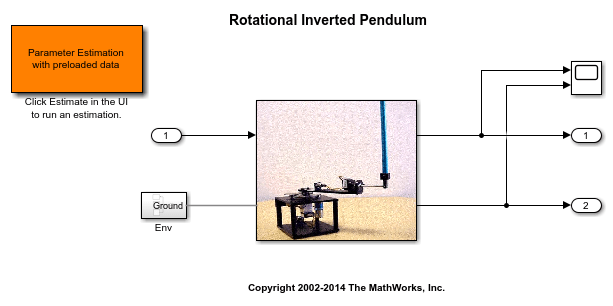
Inverted Pendulum Model Description
The pendulum system has an arm that swings in the horizontal plane, driven by a DC motor. The purpose of the arm is to provide a balancing torque to a swinging pendulum, to keep the pendulum in an upright position. The angle of both the arm and pendulum is monitored and used as feedback to control the motion of the system. For this example we will only concentrate on estimating parameters of the uncontrolled system shown below.
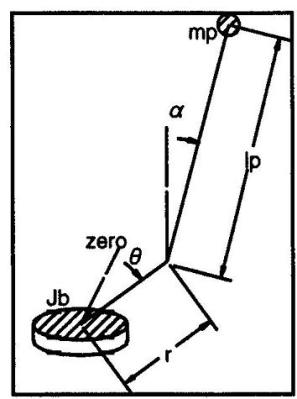
The system is modeled using Simscape Multibody. There are two bodies modeled in this system. The machine consists of one body representing the rotational arm and the other representing the pendulum. The bodies are connected by revolute joints that constrain the motion of the bodies relative to each other. An input voltage is delivered to a DC motor that provides the torque to the rotational arm.
The motor is modeled as a torque gain Kt. The arm of the pendulum has mass Ma, inertia Jb and length r. The pendulum has length lp and mass mp. For this example damping is modeled in the revolute joints using gains Kda and Kdp. The outputs of the system are the angles of the arm and the pendulum.
For this example we will run two estimations using different parameter sets for each estimation. This allows us to customize our estimation and can result in a more efficient solution.
Estimation Data
Double-click the orange block in the upper left corner of the inverted pendulum model to launch the Parameter Estimator, pre-loaded with data for this project. This is configured with measured experiment data Estimation. For other uses you can import experimental data sets from various sources including MATLAB® variables, MAT files, Excel® files, or comma-separated-value files. It is also configured with validation data Validation which we will use later, after estimation. The measured data in Estimation is shown in the experiment plot. There is only one data set used for estimation in this example.
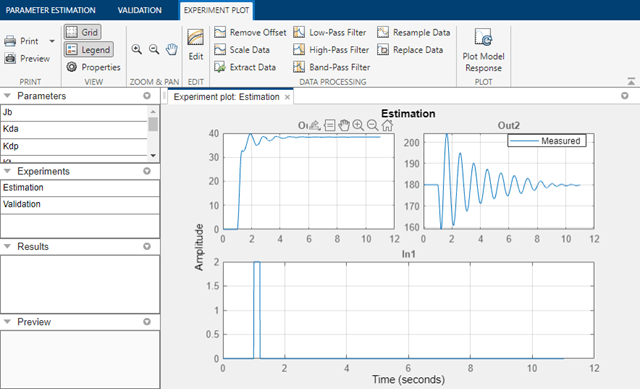
The experiment plot is also used to see how well the measured data matches the current model. Click Plot Model Response in the Parameter Estimation tab to display simulated signal data on the experiment plots. The simulation does not match the measured data, showing that the model parameters need to be estimated.
Define Variables
The next step is to define the variables for the estimation. This establishes which parameters of the simulation can be adjusted, and any rules governing their values. Click Select Parameters in the Parameter Estimation tab. For our inverted pendulum example, we have already selected the torque gain parameter, Kt, for estimation. Since we know from our physical insight that this parameter can not be negative we set its lower limit to zero.
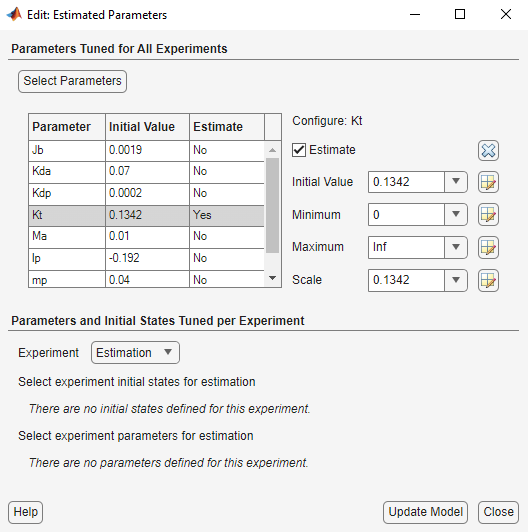
First Estimation
With the parameters for estimation specified, we select experiments to use for estimation. Click Select Experiments in the Parameter Estimation tab and select the experiment named Estimation for estimation.
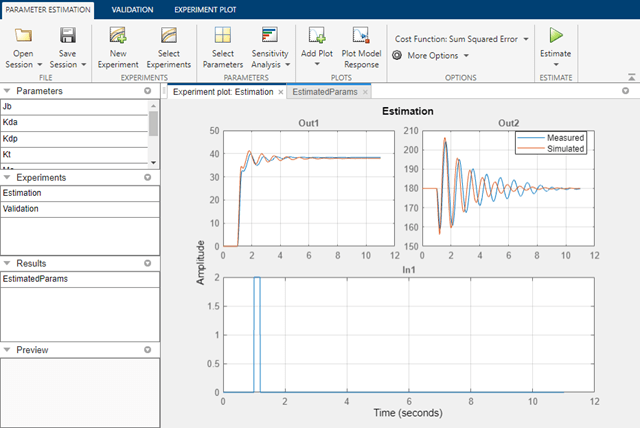
We are now ready to start our estimation. Click Estimate in the Parameter Estimation tab to start the estimation. The estimation will keep iterating the parameter value until the estimation converges and terminates.
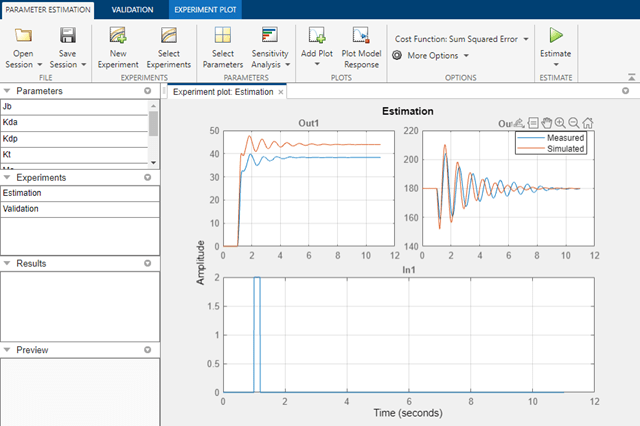
The plot below shows the experimental data overlaid with the simulated data. The simulated data comes from the model with the estimated parameter Kt. The results of the estimation show that the first output (the position of the arm) matches, however we can see that the second output (the position of the pendulum) does not show very satisfactory results. It is clear that additional estimation is needed to obtain better results.
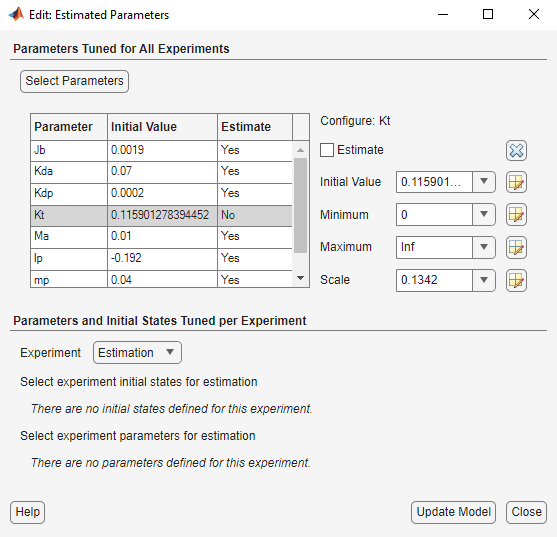
Running an Additional Estimation
This time we will leave the torque gain, Kt, constant and estimate the other parameters of the model. Click Select Parameters in the Parameter Estimation tab. Uncheck Kt, and check the other parameters as shown below.
Click Estimate to start the new estimation. The results of the second estimation are shown below.
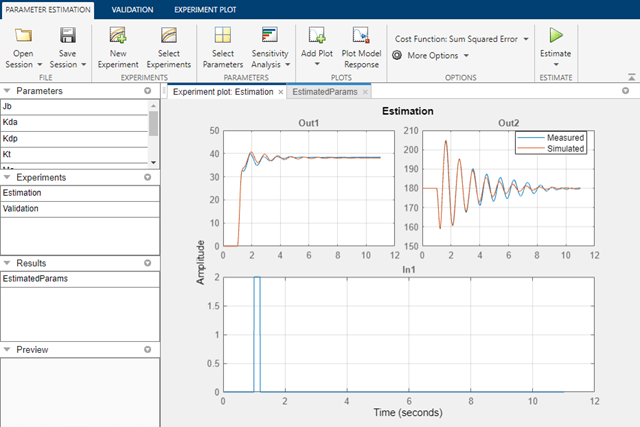
This is clearly a better result. This shows that in order to complete an estimation task it is not necessary to estimate all the parameters in the model at the same time. We can run multiple estimations keeping some parameters constant while varying others.
Validation
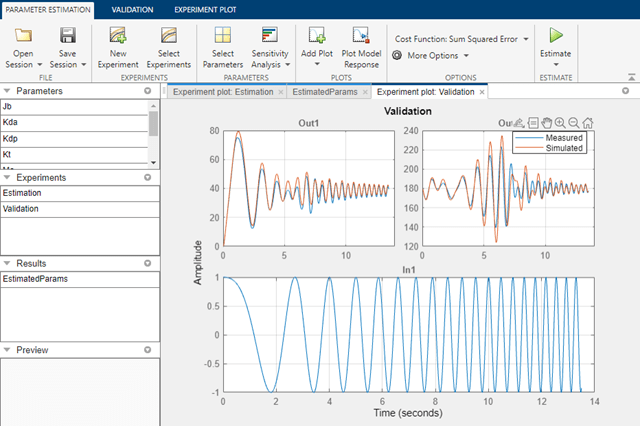
It is important to validate the results against other data sets. A successful estimation will not only match the experimental data that was used for estimation, but also the other data sets that were collected in experiments. An experiment named Validation has already been created for this project. Click Add Plot in the Parameter Estimation tab and select Validation to view the data.
Click Plot Model Response to see the simulation output overlaid on the data. The figure below shows how the inverted pendulum system responds to the validation input data. The validation shows that this model does handle the lower frequencies of the input validation data well and the model parameters were successfully estimated.
Conclusion
This example shows the flexibility of Parameter Estimation for segmenting an estimation task into multiple estimations. This allows for estimations to be run on different parameter sets which can help in the speed of estimating a given model.
Close the model.
